Cousins In Binary Tree 2

By atharvaparab9160

Problem Statement:

Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins’ values.

Two nodes of a binary tree are cousins if they have the same depth with different parents.

Return the root of the modified tree.

Note that the depth of a node is the number of edges in the path from the root node to it.

Example 1:

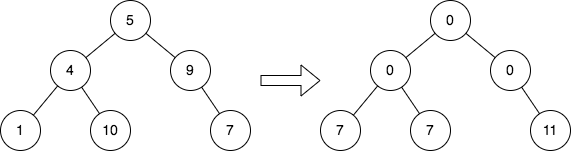
Input: root = [5,4,9,1,10,null,7]

Output: [0,0,0,7,7,null,11]

Explanation:

The diagram above shows the initial binary tree and the binary tree after changing the value of each node.

• Node with value 5 does not have any cousins so its sum is 0.
• Node with value 4 does not have any cousins so its sum is 0.
• Node with value 9 does not have any cousins so its sum is 0.
• Node with value 1 has a cousin with value 7 so its sum is 7.
• Node with value 10 has a cousin with value 7 so its sum is 7.
• Node with value 7 has cousins with values 1 and 10 so its sum is 11.

Example 2:

Input: root = [3,1,2]

Output: [0,0,0]

Intuition :

The diagram above shows the initial binary tree and the binary tree after changing the value of each node.

• Node with value 3 does not have any cousins so its sum is 0.
• Node with value 1 does not have any cousins so its sum is 0.
• Node with value 2 does not have any cousins so its sum is 0.

Complexity:

Time Complexity:O(N)

Space Complexity:O(H)

Solution:

def replaceValueInTree(root):
    def dfs(arr):
        if not arr:
            return

        total_sum = 0
        for node in arr:
            if not node:
                continue
            if node.left:
                total_sum += node.left.val
            if node.right:
                total_sum += node.right.val

        childArr = []
        for node in arr:
            curSum = 0
            if node.left:
                curSum += node.left.val
            if node.right:
                curSum += node.right.val

            if node.left:
                node.left.val = total_sum - curSum
                childArr.append(node.left)
            if node.right:
                node.right.val = total_sum - curSum
                childArr.append(node.right)

        dfs(childArr)

    root.val = 0
    dfs([root])
    return root

"""
INTUITION :

The code is designed to replace the value of each node in a binary tree with a new value that depends on its sibling nodes. Specifically, for each node, the new value is calculated as the sum of the values of all child nodes across the current level, excluding the current node's children.

Here's the intuition broken down step-by-step:

Current Node's Children Influence: For each node at a certain level, we look at the sum of all child nodes at that level (across all nodes at the same level).

Replacement Calculation: The node's left and right child values are replaced by the sum of all child nodes at that level minus the sum of their own children. In essence, each child node receives the sum of its "cousins" (children of its parent's sibling nodes).

Level-by-Level Traversal: The replacement process happens one level at a time, similar to a breadth-first traversal (BFS), but using DFS recursion to traverse down the tree while calculating and setting new values for each child node based on its cousins.

Root Initialization: The root node is initialized to 0, as it has no cousins at its level.
"""